کاربرد تکنیک های حافظه برای حفظ سریع فرمول های ریاضی و مثلثاتی
کاربرد تکنیک های تقویت حافظه در دروس ذهنی و فرمول وار از قبیل ریاضی و فیزیک می تواند در یادآوری سریع قواعد و فرمول های کلیدی کمک بسیار خوبی باشد. تعداد تکنیک های قابل ساخت بسیار زیاد است و بستگی به ذوق و مهارت درس آموز در پیوند زنی مفاهیم پیچیده و مجرد با مفاهیم ملموس و ساده دارد. نکته مهم این است که هرگز نباید فراموش کنید که حافظه خوب با یادگیری خوب تفاوت دارد. حافظه کمک کار شماست برای اینکه یادگیری تان سریع رخ دهد. به خاطر بسپارید که نظام یادگیری در عین حال که به سرعت و درستی پدیده یادسپاری ـ یادآوری متکی است اما نهایت این خود شمائید که باید فرمول های به یاد آورده شده را تحلیل و پردازش کنید.
اما در عین حال هیچ کس نمی تواند انکار کند که حافظه سریع تر به معنای پردازش جامع تر و سریع تر و سرعت عمل بیشتر و استفاده بهتر و کامل تر از فرصت هاست. فرصت هایی که هرگز معطل افراد کم حافظه نمی مانند و برعکس همیشه برای شکار شدن توسط افراد سریع الحافظه در دسترسند.
در این جا می خواهیم ارتباط بین توابع معروف مثلثاتی یعنی سینوس و کسینوس و تانژانت و کتانژانت و کسکانت و سکانت که به ترتیب عکس سینوس و کسینوس هستند با یک شکل ساده و سه قانون کلیدی و قابل حفظ برایتان رمز بندی کنیم. شکل همان فرم ساده شده و قابل فهم است و فرمول ها همان مفاهیم به ظاهر پیچیده ای هستند که پذیرش آنها برای مغز به خاطر ملموس نبودن و غریب بودن سخت است.
در شکل زیر تعریف این توابع اساسی مثلثات را می بینیم.
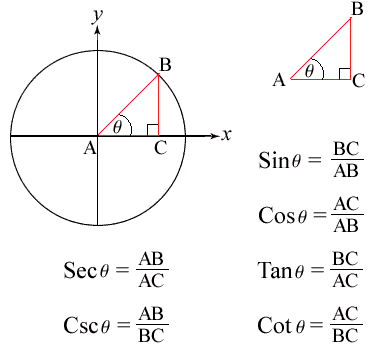
و همانطور که از این تعریف ها برمی آید روابط زیر بین این توابع برقرار است
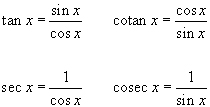
حال فرض کنید این شش تابع اساسی را روی دایره ای به شکل زیر می چینیم. با کمک سه قانون کلیدی که در تصاویر زیر آمده است مشاهده می کنید که یادگیری این روابط به ظاهر سخت بخصوص برای تازه کارهای دنیای مثلثات چقدر راحت و سریع و ساده می شود!
تبریک می گوئیم شما دارید از تکنیک های مدیریت و تقویت حافظه کوانتومی برای حفظ روابط توابع اساسی مثلثات استفاده می کنیم.
در این جا می خواهیم ارتباط بین توابع معروف مثلثاتی یعنی سینوس و کسینوس و تانژانت و کتانژانت و کسکانت و سکانت که به ترتیب عکس سینوس و کسینوس هستند با یک شکل ساده و سه قانون کلیدی و قابل حفظ برایتان رمز بندی کنیم. شکل همان فرم ساده شده و قابل فهم است و فرمول ها همان مفاهیم به ظاهر پیچیده ای هستند که پذیرش آنها برای مغز به خاطر ملموس نبودن و غریب بودن سخت است.
در شکل زیر تعریف این توابع اساسی مثلثات را می بینیم.
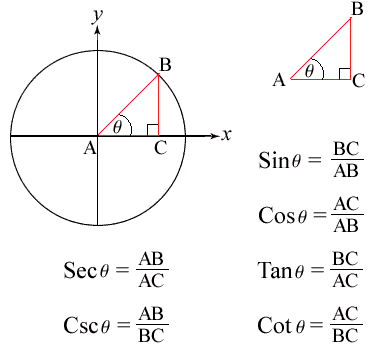
و همانطور که از این تعریف ها برمی آید روابط زیر بین این توابع برقرار است
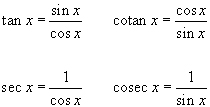
حال فرض کنید این شش تابع اساسی را روی دایره ای به شکل زیر می چینیم. با کمک سه قانون کلیدی که در تصاویر زیر آمده است مشاهده می کنید که یادگیری این روابط به ظاهر سخت بخصوص برای تازه کارهای دنیای مثلثات چقدر راحت و سریع و ساده می شود!
تبریک می گوئیم شما دارید از تکنیک های مدیریت و تقویت حافظه کوانتومی برای حفظ روابط توابع اساسی مثلثات استفاده می کنیم.
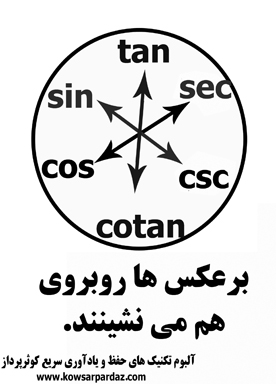
تانژانت عکس کتانژانت است و ضرب آن دو در هم مساوی یک می شود.
به همین ترتیب سکانت عکس کسینوس و کسکانت عکس سینوس است.
و همانگونه که از شکل بالا مشخص است توابع عکس روبروی هم نشسته اند.
مار از پونه خوشش می آید درست روبروی خونه اش می نشیند!
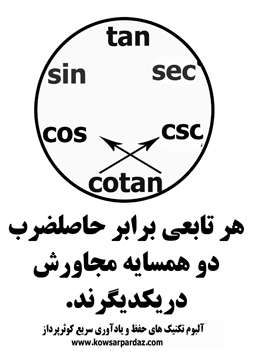
هر تابعی در چیدمان دایره ای ما برابر حاصلضرب دو همسایه مجاورش در یکدیگرند.
همسایه دو طرف با هم زدوخورد می کنند و تابع وسط از این مسیر هویت می یابد.
جالب است نه؟!
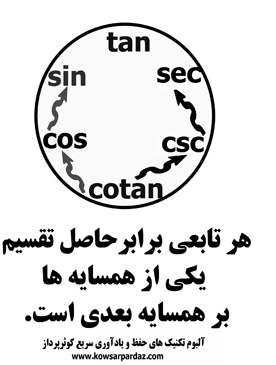
یکی از همسایه ها را بر همسایه آن سمتی و بعدی اش تقسیم کن تابع جایی که هستید بدست می آید.
باید هم بر همسایه اون سمتی اش تقسیم کرد چون همسایه این سمتی اش که خود ما هستیم!
******
همانگونه که گفتیم کاربرد تکنیک های تقویت حافظه کوانتومی کوثرپرداز در سهل الفهم سازی روابط پیچیده ریاضی و فیزیک و شیمی بستگی مستقیم به هنر و مهارت شما در یادگیری اصول اساسی این تکنیک ها دارد. باز هم در این رابطه مثال و نمونه خواهیم زد.
-------
*****
یک مثال جالب دیگر برای یادسپاری ترتیب ارقام و اعداد و حروف در یک فرمول ریاضی و فیزیک پیشرفته رابطه سینوس و کسینوس سه برابر یک زاویه است. روابط زیر را داریم
sin(3x)=3sinx-4sin3xcos(3x)=4cos3x-3cosx
برای اینکه ترتیب ضریب و توان را در این رابطه حفظ کنیم به پیوند زنی زیر به یک موضوع آشنا توجه کنید:
فرض کنید سینوس از جنس مردها باشد و کسینوس از جنس زنانه.
حال فرض کنید مردها می خواهند ده نفره فوتبال بازی کنند. آقایان بنا به روحیه تهاجمی تر خود طبیعی است که تعداد نیروهای خط وسط را بیشتر می کنند. اما خانم ها در خط دفاع بیشتر نیرو می کارند.
حمله وسط دفاع
3 4 3 -------> آقایان
3 3 4 ---------> خانم ها
همانطوری که می بینید به راحتی تکلیف ضریف و توان 3 در روابط فوق مشخص شد و اگر هم دانش آموز یا دانش جو یادش رفت. با یاد یاری این پیوند ساده به راحتی ضرایب به خاطرش می آید.
************
یادیار جالب دیگری که از تکنیک های تقویت حافظه برای آن استفاده شده است، یاد یار مکان جسم و تصویر در آینه های مقعر و عدسی های محدب است. روش کار این است که مانند شکل زیر به هم مکان یک عدد نسبت می دهیم. (دقت شود این عدد یک اسم است فاصله نیست!)
حال بر اساس اصل عدد مکان جسم+عدد مکان تصویر=8 شود می توان بلافاصله در کسری از ثانیه مکان جسم و تصویر را گفت و حقیقی بودن و وارون بودن جسم و تصویر نسبت به یکدیگر را و همین طور جهت حرکت آن به سمت یکدیگر را سریعا یافت.
حال بر اساس اصل عدد مکان جسم+عدد مکان تصویر=8 شود می توان بلافاصله در کسری از ثانیه مکان جسم و تصویر را گفت و حقیقی بودن و وارون بودن جسم و تصویر نسبت به یکدیگر را و همین طور جهت حرکت آن به سمت یکدیگر را سریعا یافت.
- لینک منبع
تاریخ: یکشنبه , 03 آذر 1398 (15:27)
- گزارش تخلف مطلب
